RADEIR: GEORG CANTOR : MATEMÁTICO

sábado, 23 de junho de 2012

GEORG CANTOR : MATEMÁTICO

George Cantor
Matemática


Dados gerais
Nome de nascimento	George Ferdinand Ludwig Philipp Cantor
Nacionalidade	Russo
Residência	Rússia (1845–1856), Alemanha (1856–1918)

Nascimento	3 de Março de 1845
Local	São Petersburgo

Falecimento	6 de Janeiro de 1918 (72 anos)
Local	Halle an der Saale

Actividade
Campo(s)	Matemática
Instituições	Universidade de Halle-Wittenberg
Alma mater	Instituto Federal de Tecnologia de Zurique, Universidade Humboldt de Berlim

Tese	1867: De aequationibus secundi gradus indeterminatis
Orientador(es)	Ernst Kummer e Karl Weierstrass
Conhecido(a) por	Conjunto de Cantor, Poeira de Cantor, Argumento de diagonalização de Cantor, Teorema de Cantor-Bernstein-Schroeder

Prêmio(s)	Medalha Sylvester (1904)

ver

George Ferdinand Ludwig Philipp Cantor (São Petersburgo, 3 de Março de 1845 — Halle, 6 de Janeiro de 1918) foi um matemático russo de origem alemã.

Conhecido por ter elaborado a moderna teoria dos conjuntos. Foi a partir desta teoria que chegou ao conceito de número transfinito, incluindo as classes numéricas dos cardinais e ordinais, estabelecendo a diferença entre estes dois conceitos, que colocam novos problemas quando se referem a conjuntos infinitos.

Nasceu em São Petersburgo (Rússia), filho do comerciante dinamarquês, George Waldemar Cantor, e de uma musicista russa, Maria Anna Böhm. Em 1856 sua família mudou-se para a Alemanha, continuando aí os seus estudos. Estudou no Instituto Federal de Tecnologia de Zurique. Doutorou-se na Universidade de Berlim em 1867. Teve como professores Ernst Kummer, Karl Weierstrass e Leopold Kronecker.

Em 1872 foi docente na Universidade de Halle-Wittenberg, na cidade alemã Halle an der Saale, onde obtém o título de professor em 1879. Toda a sua vida irá tentar em vão deixar a cidade, tendo acabado por pensar que era vítima de uma conspiração.

Cantor provou que os conjuntos infinitos não têm todos a mesma potência (potência significando "tamanho"). Fez a distinção entre conjuntos numeráveis (ou enumeráveis) (em inglês chamam-se countable - que se podem contar) e conjuntos contínuos (ou não-enumeráveis) (em inglês uncountable - que não se podem contar). Provou que o conjunto dos números racionais Q é (e)numerável, enquanto que o conjunto dos números reais IR é contínuo (logo, maior que o anterior). Na demonstração foi utilizado o célebre argumento da diagonal de Cantor ou método diagonal.

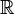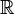Nos últimos anos de vida tentou provar, sem o conseguir, a "hipótese do contínuo", ou seja, que não existem conjuntos de potência intermédia entre os numeráveis e os contínuos - em 1963, Paul Cohen demonstrou a indemonstrabilidade desta hipótese. Em 1897, Cantor descobriu vários paradoxos suscitados pela teoria dos conjuntos. Foi ele que utilizou pela primeira vez o símbolo $\mathbb{R}$ - para representar o conjunto dos números reais.

Durante a última metade da sua vida sofreu repetidamente de ataques de depressão, o que comprometeu a sua capacidade de trabalho e o forçou a ficar hospitalizado várias vezes. Provavelmente ser-lhe-ia diagnosticado, hoje em dia, um transtorno bipolar - vulgo maníaco-depressivo.

A descoberta do Paradoxo de Russell conduziu-o a um esgotamento nervoso do qual não chegou a se recuperar. Começou, então, a se interessar por literatura e religião. Desenvolveu o seu conceito de Infinito Absoluto, que identificava a Deus. Ficou na penúria durante a Primeira Guerra Mundial, morrendo num hospital psiquiátrico em Halle.

Os conceitos matemáticos inovadores propostos por Cantor enfrentaram uma resistência significativa por parte da comunidade matemática da época. Os matemáticos modernos, por seu lado, aceitam plenamente o trabalho desenvolvido por Cantor na sua teoria dos conjuntos, reconhecendo-a como uma mudança de paradigma da maior importância.

Nas palavras de David Hilbert:

"Ninguém nos poderá expulsar do Paraíso que Cantor criou."

Ligações externas

Cantor nasceu em Saint-Petersburg, no dia 3 de Março de 1845, e passou a maior parte da sua vida na Alemanha. Como desde muito cedo revelou talento e gosto pela matemática, o seu pai decidiu que havia de ser um grande engenheiro.

Quando fez onze anos a família mudou-se para Frankfurt e Georg foi enviado para o Instituto Superior Politécnico Grand-Ducal para estudar engenharia. Embora já sentisse não ser essa a sua verdadeira vocação, era ainda muito novo para se manifestar contra a vontade do pai e contrariar as ambições que a família tinha em relação a si. No entanto, ao fim de dois anos, mais certo das suas preferências e encorajado pelo afastamento da influência directa do pai, escreveu-lhe a pedir autorização para se tornar matemático, autorização que só lhe foi concedida dois anos depois quando estava já prestes a graduar-se.

Georg ficou tão feliz que escreveu ao pai uma carta de agradecimento em que prometia fazer tudo o que estivesse ao seu alcance para lhe provar que merecia a confiança que em si ele depositava e para que toda a família pudesse vir a orgulhar-se dele.

Em 1862 Georg viajou para Zurique para continuar os seus estudos, mas voltou para casa ainda nesse ano devido à morte do pai; ingressou em Setembro na Universidade de Berlim, para estudar Matemática, Física e Filosofia. Aí teve como professores matemáticos tão brilhantes como Kummer, Weierstrass e Kronecker.

Cantor doutorou-se em 1867, tendo ficado a leccionar Matemática numa escola privada feminina devido à falta de lugares disponíveis na universidade. Só dois anos depois ingressou na Faculdade da Universidade de Halle, uma instituição de ensino pouco prestigiada.

Cinco anos depois, com 29 anos de idade, casou com Vally Guttmann, de quem teve 6 filhos; passou uma lua de mel idílica em Interlaken, na Suíça, onde conheceu e se tornou amigo de um outro jovem matemático: Richard Dedekind, que dois anos antes tinha publicado a sua própria teoria sobre os irracionais.

Os dois homens passaram muitas horas discutindo as respectivas teorias, mas ainda mais importante do que a troca de ideias foi o encorajamento que deram um ao outro, uma vez que ambos eram relativamente desprezados, ou pelo menos indiferentes, ao resto da comunidade matemática e acabavam por receber a paga que recebem todos aqueles cujas ideias são demasiado geniais para a sua época: a relegação para posições obscuras e mal remuneradas.

Cantor publicou o seu primeiro ensaio sobre a teoria de conjuntos ainda nesse ano. O ensaio tinha sido apresentado e aprovado meses antes, mas um dos editores do jornal onde ele estava para ser publicado deliberadamente atrasou a sua publicação. O editor era Leopold Kronecker, um dos professores de Cantor na Universidade de Berlim, e este atraso não foi apenas uma questão de desleixo da sua parte: era um bocadinho de maliciosa censura académica e um bocado ainda maior de ciúme profissional.

Kronecker é famoso, entre outras coisas, pela afirmação:

Deus fez os inteiros; o resto é invenção humana.

(Kronecker, cit in Muir, 1996, p. 235, trad. livr

Ele acreditava nisto sinceramente; os números negativos, fraccionários, imaginários e especialmente os números irracionais eram para si uma maldição, a fonte de todos os problemas dos matemáticos, e chegou mesmo a defender que fossem completamente banidos. Deste modo, o infinito só podia ser visto como um processo, nunca como um número: uma entidade matemática que não pudesse ser construída num número finito de passos não fazia sentido, a seu ver.

Como se pode constatar, os seus pontos de vista eram totalmente opostos aos de Cantor, e Kronecker tirou partido do seu estatuto de superioridade profissional para suprimir a heresia Cantoriana.

Mas Cantor não foi o único objecto da opressão de Kronecker. Outro matemático da Universidade de Berlim, Weierstrass, colega de Kronecker mas oponente nas suas ideias, foi profundamente ferido pelos seus ataques. No fim da sua carreira, Weierstrass chegou mesmo a escrever:

Já não consigo ter o mesmo prazer que tinha antes, quando dava aulas; Kronecker usa a sua autoridade para proclamar que todos nós, que temos trabalhado até agora para estabelecer a teoria das funções [proximamente relacionada com o infinito] somos pecadores perante Deus...

Tal veredicto, vindo de um homem cujo talento eminente e o notável desempenho na investigação matemática admiro tão sinceramente e com tanto prazer (...), é não só humilhante... como um apelo directo às novas gerações para que abandonem os seus actuais mestres e para que se reúnam à sua volta como discípulos de um novo sistema que é inevitável.

Isto é verdadeiramente triste, e provoca-me uma amarga dor, ver um homem cuja glória permanece imaculada, deixar-se arrastar a si próprio... para proclamações de cujos efeitos injuriosos sobre os outros parece não se aperceber.

(Weierstrass, cit in Muir, 1996, p. 236, trad. livre

Não se sabe ao certo até que ponto as acções de Kronecker eram motivadas por convicções intelectuais ou por ciúmes profissionais. Certamente havia um pouco de ambas. Mas embora Kronecker pudesse dificultar a vida a Weierstrass, não podia prejudicá-lo realmente a nível profissional pois a sua posição era já demasiado segura para isso. No entanto, com Cantor as coisas eram diferentes visto ser apenas um simples professor de uma universidade pouco prestigiada.

Cantor efectuou várias candidaturas para um cargo em Berlim, que foram sucessivamente recusadas, graças à forte influencia exercida por Kronecker.

Cantor acreditava que todos os prejuízos que lhe foram causados tinham sido “sistematicamente estimulados por Kronecker” (Cantor, cit in Muir, 1996, p. 237, trad. livre), e não eram apenas ilusões neuróticas. Ele não foi a única pessoa a notar ser vítima de hostilidade; Minkowski, que viria a ser mais tarde professor de Einstein, observou - sem no entanto mencionar nomes - que:

É mesmo muito lamentável que a oposição por parte de um matemático muito famoso, em campos não puramente matemáticos, possa estar a interferir com os sucessos de Cantor nas suas investigações científicas.”

(Minkowski, cit in Muir, 1996, p. 237, trad. livre)

Schoenflies foi mais incisivo nas suas acusações, notando que as teorias de Cantor:

...encontraram aguçada oposição por parte de Kronecker. Não estarei a passar dos limites se disser que atitude de Kronecker foi forjada para criar a impressão de que Cantor era, como pessoa, como matemático e como professor, um corruptor da juventude... Cantor estava isolado e abandonado até mesmo por aqueles que ele respeitava profundamente, até por Weierstrass.

(Schoenflies, cit in Muir, 1996, p. 237, trad. livre)

Cerca de 1884, grande parte das teorias de Cantor tinham sido publicadas e quase completamente ignoradas, graças à conivência de Kronecker. Uma das poucas pessoas que não as ignorou foi um jovem escandinavo chamado Mittag-Leffler. Foi a ele que Cantor confessou todos os seus problemas, escrevendo-lhe durante um ano cerca de uma carta por semana a queixar-se da perseguição por parte de Kronecker. Mas, por essa altura, era já demasiado tarde. Os ataques agressivos de Kronecker tinham-se tornado insuportáveis. Cantor nunca tinha sido muito assertivo, na sua relação com o pai sempre se submeteu docilmente, e agora mais uma vez estava a ser submetido por outro ser humano.

Tal como todos os dominados, perdeu completamente a sua auto-estima, ficou profundamente deprimido e perdeu toda a fé em si próprio e no seu trabalho. Nem mesmo as palavras de Minkowski o conseguiram animar:

As gerações futuras

vão considerar Cantor como um dos mais profundos

pensadores matemáticos desta época.

(Minkowski, cit in Muir, 1996, p. 238, trad. livre)

Na Primavera de 1884, Cantor teve um esgotamento nervoso. Foram feitas umas tréguas temporárias entre os dois homens e a saúde de Cantor melhorou. Em 1885 era ele próprio outra vez excepto numa coisa: nunca mais escreveu; a sua criatividade parecia ter-se esgotado e durante o resto da sua vida só publicou mais três ensaios.

Os ataques de Kronecker rapidamente recomeçaram, mais ferozes do que nunca: dedicou as suas conferências a devastar as teorias de Cantor, continuou as suas intrigas para o manter afastado em Halle, e eliminou todos os artigos de Cantor do Crelle’s Journal, do qual era editor.

Em 1981 Kronecker morreu e a sua influência maléfica foi desaparecendo gradualmente. Lentamente Cantor começou a receber o reconhecimento que merecia - depois de ter esperado mais de 20 anos. Foi então nomeado membro honorário da London Mathematical Society, eleito membro correspondente da Sociedade de Ciências em Gottingen, e em 1904 foi homenageado com uma medalha pela Royal Society of London.

Recordando a sua experiência recente, Cantor estava sempre pronto com uma palavra de apreço ou encorajamento para aqueles homens que continuavam a lutar. Em complemento fundou um jornal, o Deutsche Mathematiker-Vereinigung, como veículo para os trabalhos de jovens investigadores que pudessem não conseguir impor-se nos jornais controlados pelos matemáticos estabelecidos.

Para ele, no entanto o reconhecimento chegou tarde demais; a infelicidade e amargura de tantos anos não podiam ser apagadas por um súbito jorro de fama e glória. Respeitado por todo o mundo, sentiu-se como um estrangeiro no seu próprio país:

Os Alemães não me conhecem,

e no entanto eu vivi entre eles durante 52 anos.
(Cantor, cit in Muir, 1996, p. 239, trad. livre)

Cantor nunca chegou a receber um posto melhor do que aquele que tinha em Halle pois estava já demasiado velho e doente para ir para outro lugar. Os seus ataques nervosos tornaram-se mais frequentes e mais prolongados, até ter sido obrigado a resignar-se. Com 72 anos de idade, Georg Cantor morreu num hospital psiquiátrico, no dia 6 de Janeiro de 1918.